Hàm số đồng phát triển thành bên trên r dạng toán học tập cần thiết vô toàn bộ lịch trình học tập cấp cho 3. Hãy ghi lưu giữ công thức để sở hữu bài xích thi đua trung học phổ thông rất tốt và điểm tối đa.
Trong toán học tập, kiến thức và kỹ năng về hàm số đồng phát triển thành và nghịch ngợm phát triển thành bên trên một quãng r là cơ phiên bản và cần thiết. Nó phát triển thành một dạng bài xích luyện xuất hiện tại ở đa số những bài xích thi đua trung học phổ thông vương quốc. Vậy hàm số đồng biến trên r là gì? hàm nghịch ngợm phát triển thành bên trên r là gì? Hãy nằm trong thayphu mò mẫm hiểu ngay lập tức nội dung bài viết tiếp sau đây nhé!
Bạn đang xem: Hàm số đồng biến trên R và hàm nghịch biến trên R
Thế nào là là hàm số?
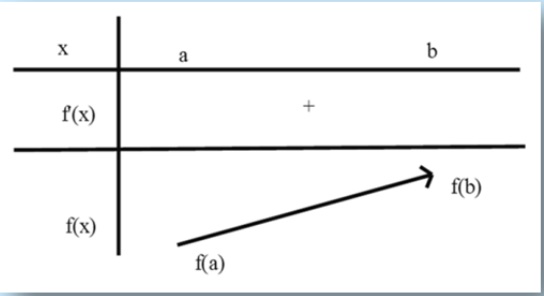
Hàm số đang được mang đến vô bài xích toán
Nếu mang đến X và Y' là nhị tụ hợp ngẫu nhiên, f tiếp tục mang đến ứng với x Ɛ X và chỉ Lúc hắn Ɛ Y mộ hàm kể từ X và Y thì thời điểm hiện nay tao sẽ sở hữu được phương trình sau:
ƒ: X → Y
Trong tình huống X và Y là những tụ hợp số, ƒ được gọi là một trong hàm số. Chúng tao chỉ quan hoài cho tới những hàm số thực của phát triển thành số thực, tức thị X và Y đều là luyện con cái của R. Tập X được gọi là luyện xác lập hoặc miền xác lập của hàm số ƒ, và thông thường được kí hiệu là D.
Biến số song lập vô tụ hợp số thực X được ký hiệu là x. Giá trị của hàm số f bên trên điểm x được ký hiệu là hắn = ƒ(x) và nằm trong tụ hợp số thực Y. Tập ăn ý toàn bộ những độ quý hiếm của hàm số ƒ Lúc x lấy từng số thực vô tụ hợp X được gọi là luyện độ quý hiếm hoặc miền độ quý hiếm của hàm số ƒ.
Một cơ hội khái niệm hàm số là: Nếu độ quý hiếm của hắn tùy thuộc vào độ quý hiếm của x sao mang đến với từng độ quý hiếm của x, và một độ quý hiếm ứng của hắn thì thời điểm hiện nay tao gọi hắn là hàm số của x thời điểm hiện nay x cũng tiếp tục là phát triển thành số của hắn.
Nếu hắn luôn luôn nhận một độ quý hiếm Lúc x thay cho thay đổi, thì hắn được gọi là hàm hằng, ví như hắn = 3.
Kí hiệu của hàm số hắn = ƒ(x) hoàn toàn có thể được đại diện thay mặt tự ƒ(x), g(x), h(x),...
Tập xác lập của hàm số hắn = ƒ(x) là luyện con cái của R bao hàm những độ quý hiếm tuy nhiên biểu thức ƒ(x) hoàn toàn có thể xác lập được.
Định lý tính đồng phát triển thành và nghịch ngợm phát triển thành của hàm số
Đầu tiên, tao cần thiết hiểu rằng nhằm một hàm số đồng biến trên r và nghịch ngợm phát triển thành thì ĐK trước tiên là hàm số cần được xác lập bên trên R.
Tính hóa học hàm đồng phát triển thành, nghịch ngợm biến
Nếu hàm số hắn = f(x) với đạo hàm bên trên khoảng tầm (a;b), thì tao hoàn toàn có thể xác lập được đặc thù đồng phát triển thành và nghịch ngợm phát triển thành của hàm số cơ. Cụ thể,
- Hàm số hắn = f(x) tiếp tục đồng phát triển thành bên trên khoảng tầm (a;b) và chỉ nếu như đạo hàm f’(x) luôn luôn ko âm bên trên khoảng tầm này. Nếu f’(x) >= 0 bên trên một vài điểm, thì con số những đặc điểm này là hữu hạn.
- Trên khoảng tầm (a;b), hàm số hắn = f(x) được xem là nghịch ngợm phát triển thành Lúc và chỉ Lúc f’(x) ≤ 0 với toàn bộ những độ quý hiếm x trong vòng cơ. Sự cân nhau xẩy ra bên trên một vài hữu hạn điểm.
- Nếu f’(x) = 0 với từng x nằm trong R thì f (x) ko thay đổi bên trên R
Chúng tao cần thiết ghi lưu giữ những tình huống rõ ràng tương quan cho tới ĐK đơn điệu bên trên R.
Hàm nhiều thức bậc 1:
- Hàm số hắn = ax + b (a ≠ 0) đồng phát triển thành bên trên ℝ ⇔ a > 0
- Hàm số hắn = ax + b (a ≠ 0) nghịch ngợm phát triển thành bên trên ℝ ⇔ a < 0
Hàm nhiều thức bậc 3:
Đây là một trong dạng Việc thịnh hành với hàm số nhiều thức bậc 3, và đa số những nội dung bài viết đều triệu tập vô tình huống này.
Xét hàm số hắn = ax^ 3 + bx^ 2 + cx + d và tính đạo hàm của chính nó theo gót công thức y’ = 3ax^ 2 + 2bx + c
Lúc này còn có nhị tình huống cần thiết xét:
- TH1 là lúc a = 0 (nếu với tham ô số)
- TH2 là lúc a ≠ 0.

Hay hoàn toàn có thể hiểu Theo phong cách viết lách cộc gọn gàng rộng lớn cơ là:

Các hàm số nhiều thức bậc chẵn thì ko thể đơn điệu bên trên trên R được.
Ví dụ minh họa
Ví dụ 1: Tìm độ quý hiếm của m sao mang đến hàm số hắn = x^3 + 2(m-1)x^2 + 3x -2 đồng phát triển thành bên trên toàn cỗ miền xác lập R.
Để hàm số hắn = x^3 + 2(m-1)x^ 2 + 3x - 2 đồng phát triển thành bên trên toàn miền R, tao cần thiết vừa lòng điều kiện:
(m-1)^2 - 3.3 ≤ 0, hoặc -3 ≤ m - 1 ≤ 3.
=> -2 ≤ m ≤ 4.
Ví dụ 2: Tìm độ quý hiếm của m nhằm hàm số hắn = mx^3 -mx^2 - (m + 4 )x + 2 nghịch ngợm phát triển thành bên trên toàn cỗ miền độ quý hiếm R.
Để mò mẫm hàm số vừa lòng đòi hỏi Việc, tao cần thiết xét nhị tình huống.
Trường ăn ý trước tiên là lúc hàm số suy biến:
Ta với m = 0 thì thì thời điểm hiện nay thay cho 0 vô m tao sẽ sở hữu được hàm số hắn = -x + 2 (là hàm hàng đầu nghịch ngợm phát triển thành bên trên toàn miền giá bán trị)
Trường ăn ý loại nhị Lúc hàm số là nhiều thức bậc 3 với m ≠ 0, và hàm số nghịch ngợm phát triển thành bên trên toàn miền độ quý hiếm Lúc và chỉ Lúc -3 ≤ m < 0.
Kết ăn ý nhị tình huống bên trên thì tao có:
-3 ≤ m ≤ 0 là ĐK nhằm hàm số vừa lòng đòi hỏi Việc.
Các dạng bài xích luyện hàm đồng phát triển thành bên trên R và hàm nghịch ngợm phát triển thành bên trên R
Dưới đó là một vài dạng bài xích luyện tương quan cho tới ĐK hàm số đồng biến trên r, nhằm những em hoàn toàn có thể vận dụng và thực hành thực tế.
Dạng 1: mò mẫm khoảng tầm đồng phát triển thành và nghịch ngợm phát triển thành của hàm số
Cho hàm số hắn = f(x)
- f’(x) > 0 ∀ x Ɛ R thì f(x) đồng biến
- f’(x) < 0 ∀ x Ɛ R thì f(x) nghịch ngợm biến
Quy tắc cho tới thực hiện một dạng bài xích tập:
- Tính f’(x)
- Giải phương trình f’(x) = 0 mò mẫm nghiệm ( x1, x2 tùy từng bài xích yêu thương cầu)
- Lập bảng xét vết nhằm mò mẫm coi hàm đồng phát triển thành hoặc nghịch ngợm phát triển thành bên trên r. Dựa vô vấn đề bảng xét vết nhằm Kết luận.
Ví dụ 1: Cho hàm số f(x) = -2x^3 + 3x^2 – 3x và 0 ≤ a < b. Tìm xác định đúng?
A. Hàm số nghịch ngợm phát triển thành bên trên ℝ
B. f (a) > f (b)
C. f (b) < 0
D. f (a) < f (b)
lời giải:
=> Ta với đạo hàm của f(x): f’(x) = -6x^2 + 6x – 3 < 0, ∀ x ∊ ℝ
Từ đạo hàm phía trên tao hoàn toàn có thể thấy được hàm số nghịch ngợm phát triển thành bên trên ℝ.
Vậy kể từ cơ tao hoàn toàn có thể => 0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)
Đáp án thực sự B
Ví dụ 2: Cho hàm số f(x) đồng phát triển thành bên trên luyện số thực ℝ, mệnh đề nào là sau đó là đúng?
A. ∀ x1 > x2 ∊ ℝ ⇒ f (x1) < f (x2)
B. ∀ x1, x2 ∊ ℝ ⇒ f (x1) > f (x2)
C. ∀x1, x2 ∊ ℝ ⇒ f (x1) < f (x2)
D. ∀x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2)
Lời giải:
Theo như đề bài xích đang được mang đến f(x) đồng phát triển thành bên trên luyện số thực ℝ. Dựa vô lý thuyết đang được học tập tao có:
⇒ x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2) vậy đáp án thực sự D
Xem thêm: NaOH + NaHCO3 → Na2CO3 + H2O
Dạng 2: Điều khiếu nại của thông số m
-
Nếu f’(x) ≥ 0, ∀ x ∊ (a;b) thì hàm số đồng phát triển thành bên trên khoảng tầm (a;b).
-
Nếu f’(x) ≤ 0, ∀ x ∊ (a;b) thì hàm số nghịch ngợm phát triển thành bên trên khoảng tầm (a;b).
Công thức rõ ràng như sau:

- Để hàm số hắn = ax^3 + bx^2 + cx + d nghịch ngợm phát triển thành bên trên một quãng có tính nhiều năm k Lúc a > 0, thì đạo hàm phương trình y’ = 0 cần với 2 nghiệm phân biệt x1 và x2 sao mang đến khoảng cách thân thuộc bọn chúng tự k ( |x1 – x2| = k)
- Khi a < 0, nhằm hàm số đồng phát triển thành bên trên một quãng có tính nhiều năm k, phương trình y’ = 0 cần với 2 nghiệm phân biệt x1 và x2 sao mang đến khoảng cách thân thuộc bọn chúng tự k (|x1 – x2| = k).
Ví dụ 1: Khi nào là hàm số hắn = x^3 – 3x^2 + (m – 2) x + 1 luôn luôn đồng phát triển thành bên trên R.
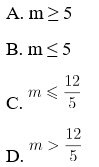
lời giải
Để hàm số đồng phát triển thành bên trên R tao giải theo gót bước sau đây:
Đạo hàm của hàm số hắn = x^3 – 3x^2 + (m – 2) x + một là y’ = 3x2 – 6x + m – 2 ≥ 0 với m là hằng số:
Ta với ∆’ = 15 – 3m => m ≥ 5 khi(∆’ ≤ 0) được thỏa mãn
Ví dụ 2: Tìm m mang đến hàm số hắn = ⅓x^3 – mx^2 – (3m + 2) x + 1 đồng phát triển thành bên trên ℝ
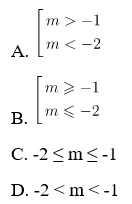
lời giải
Đạo hàm của hàm số y’ = x^ 2 – 2mx – 3m + 2 => hàm số đồng phát triển thành bên trên độ quý hiếm ℝ
⇔ x^2 – 2mx – 3m + 2 >= 0 so với từng độ quý hiếm của x vô ℝ.
Giải phương trình bậc nhị tao với ∆’ ≤ 0 ⇔ m ^ 2 + 3m + 2 ≤ 0.
=> -2 ≤ m ≤ -1. Lựa lựa chọn đáp án C
Dạng 3: Tính đơn điệu của hàm số trùng phương
Các bước nhằm phân tách thiết bị thị hàm số:
- Xác ấn định luyện xác lập của hàm số.
- Tính đạo hàm f'(x) = 0 và mò mẫm những điểm xi (i = 1, 2, ..., n) tuy nhiên bên trên cơ đạo hàm tự 0 hoặc ko xác lập.
- Sắp xếp những điểm xi theo gót trật tự tăng dần dần và lập bảng phát triển thành thiên.
- Rút rời khỏi Kết luận về những khoảng tầm đồng phát triển thành, nghịch ngợm phát triển thành của hàm số.
Ví dụ 1: Hãy phân tách tính đơn điệu của hàm số hắn = x^4 - 2x^2 + 1.Mọi độ quý hiếm của x đều vừa lòng hàm số.
Ta có: Đạo hàm y’= 4x^3 - 4x + 1= 4x (x^2 – 1)
Đặt y’ = 0 ⇒ x1 = 0, x2 = -√2/2, x3 = √2/2
Ta với bảng phát triển thành thiên
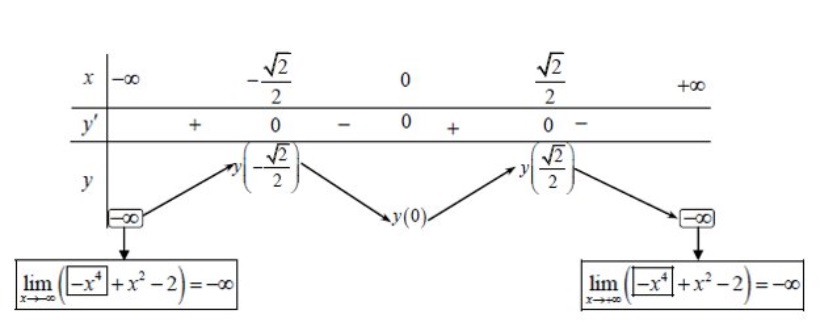
Dựa vô bảng tao hoàn toàn có thể Kết luận được:
Hàm số đồng phát triển thành bên trên khoảng tầm ( - ∞; - √2/2) và ( 0;√2/2)
Hàm số nghịch ngợm phát triển thành bên trên khoảng tầm ( - √2/2;0) và ( √2/2; + ∞)
Vận dụng những dạng bài xích nhằm thực hiện những bài xích luyện về hàm số đồng phát triển thành bên trên R
Hãy áp dụng những bài xích luyện hàm số đồng phát triển thành bên trên R nhằm hoàn toàn có thể học tập chất lượng tốt rộng lớn.
Những bài xích luyện mẫu
Bài luyện 1: Cho hàm số y=x^3+2(m-1)x^2+3x-2. Tìm m nhằm hàm đang được mang đến đồng phát triển thành bên trên R.
Lời giải
Ta với đạo hàm y’= 3x^2 + 2(m-1)x + 3-2 nhằm hàm đồng phát triển thành bên trên R thì
=> (m-1)^2 -3.3≤0 ⇔ -3≤m-1≤3
=> -2≤m≤4.
Bởi hàm nhiều thức bậc 3 với chứa chấp thông số ở thông số tối đa tao rất cần được xét ngôi trường suy phát triển thành.
Bài luyện 2: Cho hàm số y= x^3 + 2(m+1)x^2 - 3mx+5-m mò mẫm m nhằm hàm số đồng phát triển thành bên trên R
lời giải
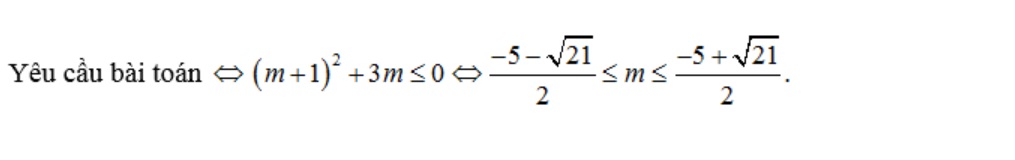
Bài luyện 3: Cho hàm số sau : 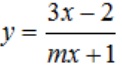 . Tìm m nhằm hàm đồng phát triển thành bên trên từng khoảng tầm xác định
. Tìm m nhằm hàm đồng phát triển thành bên trên từng khoảng tầm xác định
Lời giải:

Một số bài xích luyện về sản phẩm đồng phát triển thành và nghịch ngợm phát triển thành bên trên R về nhà
Bài luyện 1: Cho hàm số hắn = 1/3 m - 1x³ - m - 1x² - x + 1, mò mẫm m nhằm hàm số đồng phát triển thành bên trên R
Bài luyện 2: Hàm số đồng phát triển thành bên trên r Lúc nào?
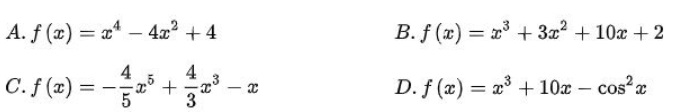
Bài luyện 3: Cho hàm số sau 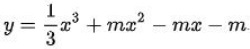 mò mẫm GTNN nhằm hàm số luôn luôn nghịch ngợm phát triển thành bên trên R
mò mẫm GTNN nhằm hàm số luôn luôn nghịch ngợm phát triển thành bên trên R
Bài luyện 4: Cho hàm số hắn = (1 - m)/3x^3 - 2mx² + 2 2 - 10x + 5 Tìm m sao mang đến hàm số luôn luôn nghịch ngợm phát triển thành bên trên R
Bài luyện 5: Tìm khoảng tầm nghịch ngợm phát triển thành của hàm số sau đây: hắn = x^4 – 6x^2 + 8x+ 1
Bài luyện 6: Cho hàm số sau: y= x^4 + 4x+ 6. Tìm khoảng tầm đồng phát triển thành của hàm số
Bài luyện 7: Cho hàm số sau: 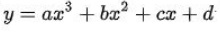 . Khi nào là hàm số đồng phát triển thành bên trên R
. Khi nào là hàm số đồng phát triển thành bên trên R
Bài luyện 8: Cho những hàm số sau đây:
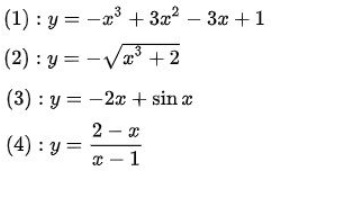
Hàm số nào là nghịch ngợm phát triển thành bên trên R?
Bài luyện 9: Tìm những độ quý hiếm của thông số m trong mỗi hàm số sau:
Xem thêm: Khái niệm, điều chế và tính chất hóa học của ankin
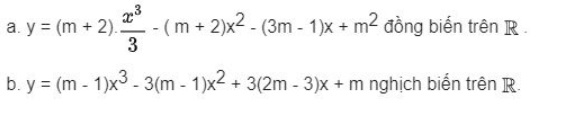
Bài luyện 10: Cho hàm số sau đây: 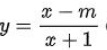 . Tìm m nhằm hàm đồng phát triển thành bên trên luyện xác lập.
. Tìm m nhằm hàm đồng phát triển thành bên trên luyện xác lập.
Kết luận
Trên đó là những kiến thức và kỹ năng về hàm số đồng phát triển thành bên trên R và hàm đồng phát triển thành bên trên R tuy nhiên thayphu mong muốn gửi cho tới những em học viên. Bài viết lách thể hiện tại cụ thể những kiến thức và kỹ năng trọng tâm và những dạng bài xích luyện thịnh hành. Hy vọng với những share này sẽ hỗ trợ những chúng ta cũng có thể nâng cấp toán học tập rộng lớn và dành riêng được thành quả cao vô kỳ thi đua tới đây.




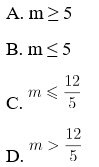
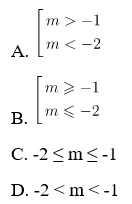

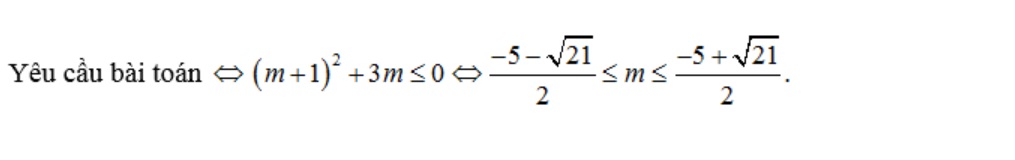
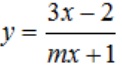 . Tìm m nhằm hàm đồng phát triển thành bên trên từng khoảng tầm xác định
. Tìm m nhằm hàm đồng phát triển thành bên trên từng khoảng tầm xác định
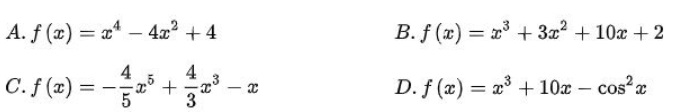
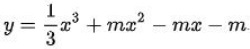 mò mẫm GTNN nhằm hàm số luôn luôn nghịch ngợm phát triển thành bên trên R
mò mẫm GTNN nhằm hàm số luôn luôn nghịch ngợm phát triển thành bên trên R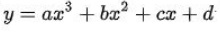 . Khi nào là hàm số đồng phát triển thành bên trên R
. Khi nào là hàm số đồng phát triển thành bên trên R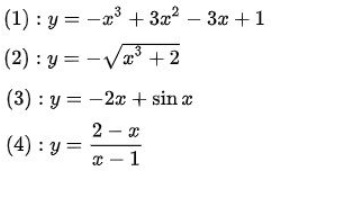
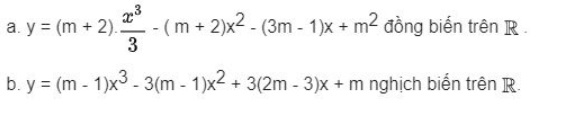
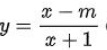 . Tìm m nhằm hàm đồng phát triển thành bên trên luyện xác lập.
. Tìm m nhằm hàm đồng phát triển thành bên trên luyện xác lập.